Ast 350L

You may have one partner for this activity, or you may do it alone. If you have a partner, please place both names on your answer sheet.

Write the date, the two locations, and show all work on your answer sheet.

A papyrus from 230 B.C. :

Eratosthenes Finds Diameter of Earth!

Alexandria Eratosthenes peered into a well
here at noon and came up with the diameter and
circumference of our planet! The summer solstice
sun and a trip to Syene was all it took...........



Objectives- Materials- Background-

Eratosthenes made a remarkably precise measurement of the size of the earth. He knew that at the summer solstice the sun shone directly into a well at Syene at noon. He found that at the same time, in Alexandria, Egypt, approximately 787 km due north of Syene (now Aswan), the angle of inclination of the sun’s rays was about 7.2°. With these measurements he computed the diameter and circumference of the earth as we will do.



Activities-

1) How did Eratosthenes get a result?

Since light rays travel parallel to each other, we get pairs of congruent
angles. With the central angle measuring 7.2° and the length of the
arc between Syene and Alexandria 787 km we can write the proportion:

7.2 / 360 = 787 / X


therefore X = 39350 km, the circumference.

Convert this value to miles: _____________________

Find the radius and diameter of the earth: (use C = 2*Pi*r )

radius: _______________ km ______________ mi
diameter: _____________ km ______________ mi

2) It's your turn!

Procedure:
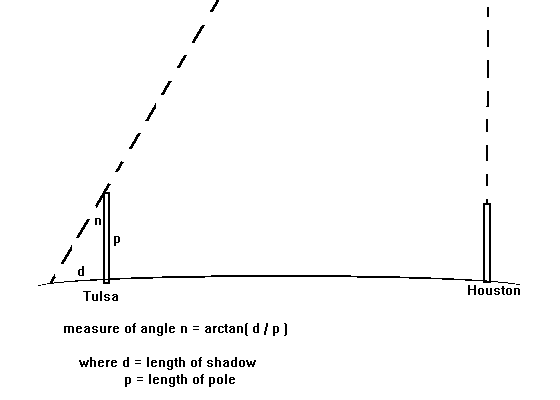
  1. Find someone that you can contact via e-mail that is at least 500 km either due north or due south.. For example, from Houston one could choose a Tulsa, Oklahoma. Using an atlas to measure the distance between them, one finds they are 705 km apart.

  2. Drive a pole into the ground at a 90 degree angle. Make sure it is in a sunny location. Measure the length of the pole from the ground to the topmost point. Write this number down.

  3. Monitor the pole at local noon, that is, when the shadow is smallest. E-mail your partner to measure the sun’s angle of inclination from the shadow cast by his/her pole and return the result. Make sure that your partner includes the length of the pole from ground to topmost point. (Use the hint at the bottom of the page to tell them when to make the measurement.) See diagram below for measurements.

  4. Using the distance value and the measured angle, compute the circumference and diameter as done in activity 1.

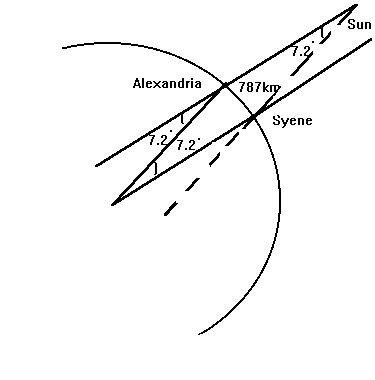
Write down the angles for each location.

( Note: There is an error in this diagram. Can you find it? )



3) Compare your results.

The earth’s average radius is usually accepted as 6.38 * 10^6 m .
Compute the percent of error for Eratosthenes’ result.

______________%

Compute the percent of error for your result.

______________%


4) Discussion questions:

  • Why do you think we need to choose two cities that lie roughly on the same longitudinal line? Why couldn’t we use New York and Los Angeles?

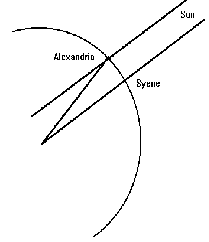
  • How did Eratosthenes measure the distance between Alexandria and Syene over 2000 years ago?

  • How could Eratosthenes know that at noon on the summer solstice in Syene the sun’s rays shown directly to the bottom of the well while at the same time in Alexandria they did not?


Hint
To find the time that the sun is highest in the sky for any day, any location, look for the "time that sun transits" at US Naval Observatory website.
Original activity authored by:
Dennis P. Donovan at Rice University 1996
Adapted by Mary Kay Hemenway, University of Texas at Austin, September 2003.